微信打开

首页

第五单元 A卷

本单元知识盘点：

1.圆的各部分名称。

 

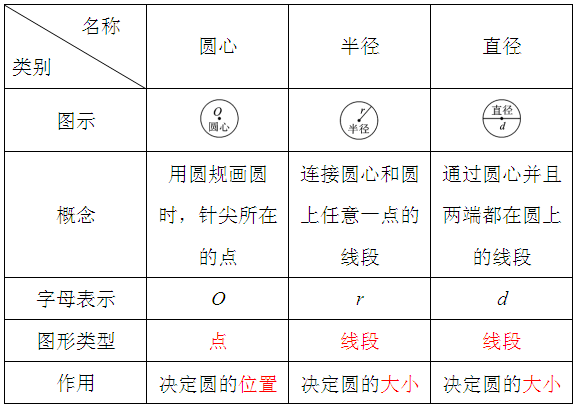
2.圆的特征。

（1）圆是由一条曲线围成的封闭图形，无顶点。

（2）在同一圆内，有无数条半径且长度都相等；有无数条直径且长度都相等。

（3）在同圆或等圆中，直径是半径的２倍，半径是直径的一半，用字母表示为ｄ＝2ｒ或ｒ＝ｄ÷２。

（4）圆是轴对称图形，它有无数条对称轴。圆的每条直径所在的直线都是它的对称轴。

3.用圆规画圆的方法。

 第一步：确定半径。把圆规的两脚分开，定好两脚间的距离。

 第二步：确定圆心。把圆规有针尖的一脚固定在一点。

 第三步：旋转一周。把圆规装有铅笔的那只脚旋转一周就画出一个圆。

4.圆的周长。

     围成圆的曲线的长是圆的周长，一般用字母C表示。圆的周长的大小与半径的长短有关。

5.圆周率。

     任意一个圆的周长与它的直径的比值是一个固定的数,我  们把它叫作圆周率，用字母 π 表示。它是一个无限不循环小数，π=３.１４１５９２６５３５……计算时， π 通常 取它的近似值３.１４。用公式表示圆周率

圆周率=圆周长/圆直径 =π。

   6.圆的周长计算公式。

     圆的周长 ＝直径×圆周率或圆的周长 ＝半径×２×圆周 率。如果用C表示圆的周长，那么C=π d或C=2π r。

   7.圆的面积。

     圆所占平面的大小叫圆的面积，一般用字母S表示。圆的面积的大小与半径的长短有关。

8.圆的面积计算公式。

      如果用S表示圆的面积，那么S = π r2或S = π( d÷2）2。

9.圆环。

     两个半径不等的同心圆之间的部分叫作圆环，也叫作环形。

10.圆环的面积计算公式。

   外圆的半径是R，内圆的半径是r，圆环的面积 ＝外圆面积－内圆面积，用字母表示为S=π R2-π r2或S=π （R2- r2）。

 11.“外方内圆”和“外圆内方”的问题。

      （1）在正方形内画一个最大的圆，这个圆的直径等于正

           方形的边长。如果圆的半径是r，那么正方形和圆之 间部分的面积为0.86r2。

      （2）在圆内画一个最大的正方形，这个正方形的对角线

           等于圆的直径。如果圆的半径是r，那么正方形和圆 之间部分的面积为1.14r2。

 12.扇形。 

      弧：圆上任意两点（如下图A、B）之间的部分叫作弧，读作弧AB。

      圆心角：由两条半径组成，顶点在圆心的角叫圆心角。如下图∠AOB。

      扇形：一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形。如下图中涂色部分就是扇形。在同一个 圆中，扇形的大小与这个扇形的圆心角的大小有关。

                    

 

 

 

 

本单元知识点易错汇总：
1.直径必须过圆心。
2.圆有无数条对称轴，每一条直径所在的直线都是它的对称轴。半圆只有1条对称轴。
3.在同一个圆内，一条直径的长度等于两条半径的长度和，但只有在同一条直线上的两长半径才能组成一条直径。
4.圆周率是任意一个圆的周长和它的直径的比值，这个比值是一个固定的数，与圆的大小无关。
5.圆周率是一个无限不循环小数，在实际应用中取它的近似值。
6.计算时如果单位不统一，一定要先统一单位，然后再计算。
7.在计算圆的面积时，r2是r×r，不是r×2。
8.圆环必须是两个同心圆形成。
9.求圆环的面积时，要先算出的是“平方差”，不是“差的平方”。
10.在正方形内画一个最大的圆，这个圆的直径等于正方形的边长，在长方形内画一个最大的圆，这个圆的直径等于长方形的宽。
11.在圆内画一个最大的正方形，这个正方形的对角线等于圆的直径。
12.圆心角必须具备两个条件：一是顶点在圆心上；二是角的两边是圆的半径。

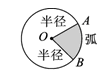
13.在同一个圆中，扇形越大，这个扇形所对的圆心角就越大。