 l 用圆规画圆的方法。
l 用圆规画圆的方法。
第一步:确定半径。把圆规的两脚分开,定好两脚间的距离。
第二步:确定圆心。把圆规有针尖的一脚固定在一点。
第三步:旋转一周。把圆规装有铅笔的那只脚旋转一周就画
l 圆的周长计算公式。
圆的周长 =直径×圆周率或圆的周长 =半径×2×圆周率。
如果用C表示圆的周长,那么C=π d或C=2π r。
l 圆的面积计算公式。.png)
l 圆环的面积计算公式。
外圆的半径是R,内圆的半径是r,圆环的面积 =外圆面积-内圆面积,用字母表示为S=πR2-πr2或S=π(R2- r2)。
l 连续求一个数的几分之几是多少的问题的解题方法。
关键是正确确定每一步中的单位“1”,注意不能把没有关系的数量和分率对应起来。
方法一:把已知量看作单位“1”,先求出已知量的几分之几,即中间量,再求出中间量的几分之几。
方法二:先求出所求量占已知量的几分之几,再用已知量乘这个分 率。
l 求比一个数量增加(或减少)几分之几的数量是多少的解题方法。
关键是找准单位“1”,可以借助线段图来分析数量关系,明确数量和分率之间的对应关系。
方法一:单位“1”的量±单位“1”的量×这个数量比单位“1”的量增加(或减少)几分之几=这个数量。
方法二:单位“1”的量×[1±这个数量比单位“1”的量增加(或减少)几分之几]=这个数量。
l 已知总量及一部分量是总量的几分之几,求另一部分量的解题方法。
l 已知比一个数多(或少)几分之几的数是多少,求这个数的实际问题的解题方法。
解题时要找准单位“1”,借助线段图分析数量关系,然后利用方程 解答,也可以根据分数除法的意义列式求解。
方程一:这个数(x)±这个数(x)×比这个数多(或少)的几分之几=已知量。
方程二:这个数(x)×[1±比这个数多(或少)的几分之几=已知量。
l 已知一部分量占总量的几分之几及另一部分量,求总量的实际问题的解题方法。
可以找出等量关系列方程求解,也可以先求出已知的部分量占总量的几分之几,然后列除法算式求解。
方程一:总量(x)-总量(x)×一部分量占总量的几分之几=另一部分量。
方程二:总量(x)×(1-一部分量占总量的几分之几)=另一部分量。
l 求比值的方法。
用比的前项除以后项,所得的商就是比值。
l 化简比的方法。
(1)整数比的化简方法。
方法一:先把比改写成分数的形式 ,再把这个分数进行约分。
方法二:比的前项和后项同时除以它们的最大公因数。
(2)分数比的化简方法。
方法一:先利用比与除法的关系,将比转化成除法算式,再求出结果,最后将得数转化成最简整数比的形式。
方法二:比的前项和后项同时乘它们分母的最小公倍数,先转化成整数比,再进行化简。
(3)小数比的化简方法。
方法一:利用比与除法的关系,将两个小数的比转化成两个小数相除的形式,根据商不变的规律,先将被除数与除数同时扩大相同的倍数(0除 外),转化成整数除法后,再进行化简。
方法二:通常把比的前、后项的小数点同时向右移动相同的位数,先转化成整数比,再进行化简。
l 按比分配的意义。
把一个数量按照一定的比进行分配,这种分配的方法叫作按比分配。
l 按比分配问题的解题方法。
方法一:先求出总份数,再求出各部分量占总量的几分之几,最后求出各部分量。
方法二:先求出每份是多少,再用每份量乘各部分量所占的份数,求出各部分量。
l 求“一个数比另一个数多(或少)百分之几”的方法。
方法一:先求出一个数比另一个数多(或少)的具体数量,再除以单位“1”的量(与哪个量相比,那个量就是单位“1”)。
方法二:先求出一个数是另一个数的百分之几,然后用这个百分数减去单位“1”(或用单位“1”减去这个百分数)。
l 求“比一个数增加(或减少)百分之几的数”的方法。

l 解决成数问题的方法。
先将成数化成百分数(几成就是十分之几,也就是百分之几十),然后按照百分数问题的解法进行解答。
l 已知两个部分量的差(或和)及两个部分量对应的百分数,求总量,这类问题用方程解有两种解法:
方法一:A%x-B%x = 两个部分量的差(A>B)或者 A%x+B%x =两个部分量的和。
方法二:(A% -B%)x =两个部分量的差(A>B)或者(A% +B%)x =两个部分量的和。
l 用方程解“已知比一个数增加(或减少)百分之几的数是多少,求这个数”这类问题有两种解法:
方法一:x×[1±比单位“1”增加(或减少)的百分数]=已知量 。
方法二:x±x×比单位“1”增加(或减少)的百分数=已知量。
l 用方程解“已知一部分量占总量的百分之几及另一部分量,求总量”这类问题有两种解法:
方法一:总量(x)×(1-已知部分量占总量的百分数)=另一部分量。
方法二:总量(x)-总量(x)×已知部分量占总量的百分数= 另一部分量。
l 解决折扣问题的方法。
先将折扣化成百分数(几折就是十分之几,也就是百分之几十;几几折就是十分之几点几,也就是百分之几十几),然后按照百分数问题的解法进行解答。
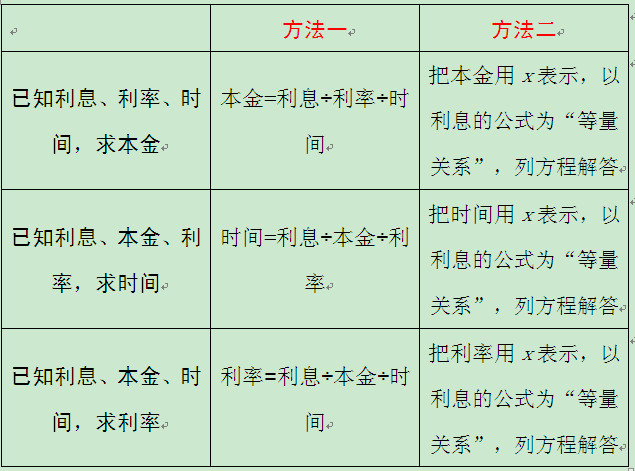
l 利息的计算公式。
利息=本金×利率×时间。
l 已知利息计算公式中的三个量,求另一个量的方法。